היפוקרטס צ'יוס (שכבתי 460 לפנה"ס) הדגים כי האזורים בצורת הירח בין קשתות עגולות, הידועים בשם נעורים, יכולים לבוא לידי ביטוי בדיוק כאזור ישראלי, או ריבוע. במקרה הפשוט הבא, שני רצועות שפותחו סביב צידי המשולש הימני יש שטח משולב שווה לזה של המשולש.
-
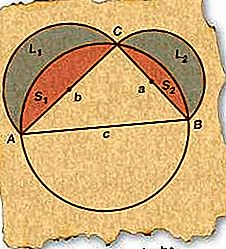
החל מ- ΔABC הימני, צייר מעגל שקוטרו עולה בקנה אחד עם AB (צד ג), היפוזה. מכיוון שצריך להיות רשום בתוך המעגל כל משולש ימני המצויר בקוטר מעגל להיפוטוזה שלו, C חייב להיות על העיגול.
-
צייר חצי עיגולים בקוטר AC (צד b) ו- BC (צד א) כמו בתמונה.
-
תייגו את הנעימות שהתקבלו L 1 ו- L 2 ואת הקטעים שהתקבלו S 1 ו- S 2, כמצוין בתמונה.
-
כעת על סכום הלהקות (L 1 ו- L 2) להיות שווה לסכום חצי המעגלים (L 1 + S 1 ו- L 2 + S 2) המכיל אותם מינוס שני הקטעים (S 1 ו- S 2). לפיכך, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (מכיוון ששטח המעגל הוא פי כפול מכיכר הרדיוס).
-
סכום הקטעים (S 1 ו- S 2) שווה לשטח מעגל החצי מבוסס על AB מינוס שטח המשולש. לפיכך, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
החלפת הביטוי בשלב 5 לשלב 4 ובחינת המונחים השכיחים, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
מכיוון ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, על ידי משפט פיתגורס. לפיכך, L 1 + L 2 = ΔABC.
ההיפוקרטס הצליח לרבוע כמה סוגים של לונס, חלקם על קשתות גדולים יותר ופחות מחצי עיגולים, והוא רמז, אם כי לא האמין, שהשיטה שלו יכולה לרבוע מעגל שלם. בסוף העידן הקלאסי ציין בוטיוס (בערך ad 470–524), שתרגומיו הלטיניים של קטעי אוקליד ישאירו את אור הגיאומטריה המהבהב במשך חצי אלף שנה, ומישהו ציין את הכיכר של המעגל. לא ידוע אם הגאון הלא נודע השתמש במנגינות או בשיטה אחרת, שכן מחוסר מקום בותיוס לא נתן את ההפגנה. בכך העביר את האתגר של ריבוע המעגל יחד עם שברי גיאומטריה שככל הנראה מועילים לביצועו. האירופאים המשיכו למשימה חסרת האונים עד להארה. לבסוף, בשנת 1775, האקדמיה למדעים של פריז, שנמאסה ממשימתה לאיתור השגיאות בפתרונות הרבים שהוגשו לה, סירבה לקיים דבר נוסף עם ריבועי מעגלים.