משוואה דיפרנציאלית, אמירה מתמטית המכילה נגזרת אחת או יותר - כלומר מונחים המייצגים את שיעורי השינוי בכמויות משתנות ברציפות. משוואות דיפרנציאליות נפוצות מאוד במדע והנדסה, כמו גם בתחומים רבים אחרים של לימוד כמותי, מכיוון שמה שניתן לצפות ולמדוד ישירות עבור מערכות העוברות שינויים הם שיעורי השינוי שלהם. הפיתרון של משוואה דיפרנציאלית הוא באופן כללי משוואה המבטאת את התלות התפקודית של משתנה אחד על אחד או יותר אחרים; בדרך כלל הוא מכיל מונחים קבועים שאינם קיימים במשוואת ההפרש המקורית. דרך נוספת לומר זאת היא שפתרון של משוואה דיפרנציאלית מייצר פונקציה שניתן להשתמש בה כדי לחזות את התנהגות המערכת המקורית, לפחות באילוצים מסוימים.

ניתוח: ניוטון ומשוואות דיפרנציאליות
יישום הניתוח הם משוואות דיפרנציאליות, הקושרות את שיעורי השינוי של כמויות שונות לערכיהם הנוכחיים,
משוואות דיפרנציאליות מסווגות למספר קטגוריות רחבות, ואלה בתורן מחולקות עוד יותר לקטגוריות משנה רבות. הקטגוריות החשובות ביותר הן משוואות דיפרנציאל רגילות ומשוואות דיפרנציאליות חלקיות. כאשר הפונקציה המעורבת במשוואה תלויה רק במשתנה יחיד, הנגזרות שלה הן נגזרות רגילות ומשוואת ההפרש מסווגת כמשוואה דיפרנציאלית רגילה. מצד שני, אם הפונקציה תלויה בכמה משתנים עצמאיים, כך שהנגזרות שלה הן נגזרות חלקיות, משוואת ההפרש מסווגת כמשוואה דיפרנציאלית חלקית. להלן דוגמאות למשוואות דיפרנציאליות רגילות:
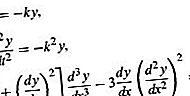
באלה, y מייצג את הפונקציה, או t או x הם המשתנה הבלתי תלוי. הסמלים k ו- m משמשים כאן כדי לעמוד על קבועים ספציפיים.
לא משנה מה הסוג, משוואת דיפרנציאליות אומרים שהיא בסדר התשיעי אם היא כוללת נגזרת של הסדר ה- n אך אין נגזרת של סדר גבוה יותר מזה. המשוואה היא דוגמא למשוואה דיפרנציאלית חלקית של הסדר השני. התיאוריות של משוואות דיפרנציאליות רגילות וחלקיות שונות באופן ניכר, ומסיבה זו מטפלים בשתי הקטגוריות בנפרד.
במקום משוואה דיפרנציאלית יחידה, מטרת המחקר עשויה להיות מערכת סימולטנית של משוואות כאלה. ניסוח חוקי הדינמיקה מוביל לעתים קרובות למערכות כאלה. במקרים רבים, ניתן להחליף באופן מיטבי משוואה דיפרנציאלית אחת של הסדר ה- n על ידי מערכת של n משוואות סימולטניות, שכל אחת מהן מהסדר הראשון, כך שניתן ליישם טכניקות מאלגברה לינארית.
משוואה דיפרנציאלית רגילה שבה למשל מציינים את הפונקציה ואת המשתנה הבלתי תלוי על ידי y ו- x היא למעשה סיכום מרומז של המאפיינים המהותיים של y כפונקציה של x. יש להניח כי מאפיינים אלה יהיו נגישים יותר לניתוח אם ניתן לייצר נוסחה מפורשת ל- y. נוסחה כזו, או לפחות משוואה ב- x ו- y (שאינה כוללת נגזרות) שניתן להסיק מהמשוואה הדיפרנציאלית, נקראת פיתרון של משוואת ההפרש. תהליך הוצאת הפיתרון מהמשוואה על ידי יישומי האלגברה והחשבון נקרא פתרון או שילוב המשוואה. עם זאת יש לציין כי המשוואות הדיפרנציאליות שניתן לפתור במפורש הן של מיעוט קטן בלבד. לפיכך, יש ללמוד את רוב הפונקציות בשיטות עקיפות. אפילו יש להוכיח את קיומה כשאין אפשרות לייצר אותו לבדיקה. בפועל, נעשה שימוש בשיטות מניתוח מספרי, הכוללות מחשבים, בכדי להשיג פתרונות מקורבים.