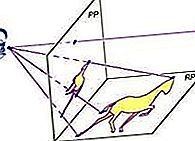
חתך חרוטי, הנקרא גם חרוט, בגיאומטריה, כל עקומה המיוצרת בצומת מישור וחרוט מעגלי ימני. תלוי בזווית המטוס ביחס לקונוס, הצומת הוא מעגל, אליפסה, היפרבולה או פרבולה. מקרים צמתיים מיוחדים (מנווונים) מתרחשים כאשר המטוס עובר רק דרך הקצה (מייצר נקודה יחידה) או דרך האפקס ונקודה נוספת על החרוט (מייצרת קו ישר אחד או שני קווים ישרים מצטלבים). ראו את הדמות.
גיאומטריה השלכתית: קטעי חרוטי השלכה
ניתן לראות בחתך החרוטי כקטעים מישוריים של חרוט מעגלי ימני (ראו איור). באמצעות
את התיאורים הבסיסיים, אך לא את שמותיהם, של מקטעי החרווט ניתן לייחס למנכמוס (פרח כ -350 לפנה"ס), תלמיד של אפלטון ואודוקסוס מקנידוס כאחד. אפולוניוס מפרגה (בערך 262–190 לפני הספירה), המכונה "הגאומטר הגדול", נתן לחלקי החרווט את שמם והיה הראשון שהגדיר את שני ענפי ההיפרבולה (אשר מניחים את הקונוס הכפול). המאמרה של שמונה נפחים של אפולוניוס על קטעי הקוניק, קוניקים, היא אחת העבודות המדעיות הגדולות ביותר מהעולם העתיק.
הגדרה אנליטית
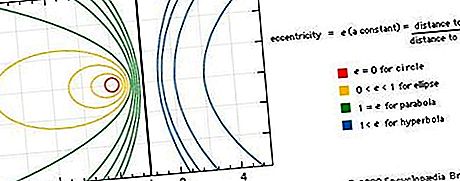
ניתן לתאר גם חרוורים כעקומות מישור שהם הנתיבים (לוקוסים) של נקודה הנעת כך שיחס המרחק שלה מנקודה קבועה (המיקוד) למרחק מקו קבוע (הכיוון) הוא קבוע, הנקרא האקסצנטריות של העקומה. אם האקסצנטריות היא אפס, העקומה היא מעגל; אם שווה לזה, פרבולה; אם פחות מאחד, אליפסה; ואם גדול מאחד, היפרבולה. ראו את הדמות.
כל קטע חרוטי מתאים לתרשים של משוואת פולינום מדרגה שנייה של הצורה Ax 2 + על ידי 2 + 2Cxy + 2Dx + 2Ey + F = 0, כאשר x ו- y הם משתנים ו- A, B, C, D, E ו- F הם מקדמים התלויים בחריש המסוים. על ידי בחירה מתאימה של צירי קואורדינטה, ניתן לצמצם את המשוואה לכל חרוט לאחת משלוש צורות r פשוטות: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1, או y 2 = 2px, המתאימים לאליפסה, היפרבולה ופרבולה, בהתאמה. (אליפסה כאשר a = b הוא למעשה מעגל.) השימוש הנרחב במערכות קואורדינטות לניתוח האלגברי של עקומות גיאומטריות מקורו ברנה דקארט (1596–1650). עיין בהיסטוריה של הגיאומטריה: גיאומטריה קרטזית.
מקורות יוונים
ההיסטוריה המוקדמת של קטעי החרווט מצטרפת לבעיה של "הכפלת הקוביה". על פי ארטוסתנס מקירנה (ca. 276–190 לפנה"ס), תושבי דלוס התייעצו עם האורקל של אפולו לצורך סיום מגיפה (כ -430 לפנה"ס) והונחו לבנות לאפולו מזבח חדש של פי שניים מנפח המזבח הישן ועם אותה צורה מעוקבת. במבוכה, הדליאנים התייעצו עם אפלטון, שאמר כי "האורקל התכוון, לא שהאל רצה מזבח בגודל כפול, אלא שהוא רצה, בהציבו להם את המשימה, לבייש את היוונים בגלל הזנחתם במתמטיקה ובזלזולם לגיאומטריה. " היפוקרטס צ'יוס (בערך 470–410 לפנה"ס) גילה לראשונה כי ניתן לצמצם את "בעיית הדליאן" כדי למצוא שני פרופורציות ממוצעות בין a ל- 2a (נפחים של המזבחות בהתאמה) - כלומר קביעת x ו- y כך ש: x = x: y = y: 2a. זה שווה לפיתרון בו זמנית של שתי משוואות x 2 = ay, y 2 = 2ax ו- xy = 2a 2, שמתאימות לשתי פרבולות והיפרבולה בהתאמה. מאוחר יותר, ארכימדס (בערך 290–211 לפנה"ס) הראה כיצד להשתמש בחתכים חרויים כדי לחלק כדור לשני מקטעים עם יחס נתון.
חוליות (כ -200 לפני הספירה) הדגימו גיאומטרית כי קרניים - למשל מהשמש - המקבילות לציר פרבוליד המהפכה (המיוצר על ידי סיבוב פרבולה סביב ציר הסימטריה שלה) נפגשות במוקד. אומרים שארכימדס השתמש בנכס זה כדי להצית ספינות אויב. את המאפיינים המוקדיים של האליפסה ציטט אנתמיוס מטראלס, אחד האדריכלים של קתדרלת האגיה סופיה בקונסטנטינופול (שהושלם בפרסומת 537), כאמצעי להבטיח שניתן יהיה להאיר את המזבח לאור השמש כל היום.