ניתוח טנסור, ענף המתמטיקה העוסק ביחסים או בחוקים שנשארים תקפים ללא קשר למערכת הקואורדינטות המשמשות לציון הכמויות. יחסים כאלה מכונים קובריאנט. טנזורים הומצאו כהרחבה של וקטורים כדי למסד את המניפולציה של ישויות גיאומטריות הנובעות מחקר סעפות מתמטיות.
וקטור הוא ישות שיש לה גם גודל וגם כיוון; ניתן לייצג אותו על ידי רישום של חץ, והוא משלב עם ישויות דומות על פי חוק המקביל. בגלל החוק הזה, לווקטור יש רכיבים - סט שונה לכל מערכת קואורדינטות. כאשר משתנים מערכת הקואורדינטות, מרכיבי הווקטור משתנים על פי חוק מתמטי של טרנספורמציה שניתן להסיק מחוק המקביל. לחוק זה של טרנספורמציה של הרכיבים יש שני תכונות חשובות. ראשית, לאחר רצף של שינויים שבסופו במערכת הקואורדינטות המקורית, רכיבי הווקטור יהיו זהים לזה בהתחלה. שנית, מערכות יחסים בין וקטורים - למשל, שלושה ווקטורים U, V, W כך ש- 2U + 5V = 4W - יהיו קיימים ברכיבים ללא קשר למערכת הקואורדינטות.
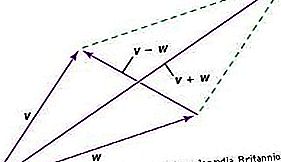
ניתן לראות אפוא וקטור כישות שיש לה במרחב n ממדי n רכיבים המשתנים על פי חוק ספציפי של טרנספורמציה שיש לו את המאפיינים הנ"ל. הווקטור עצמו הוא ישות אובייקטיבית שאינה תלויה בקואורדינטות, אך היא מטופלת במונחים של רכיבים עם כל מערכות הקואורדינטות על בסיס שווה.
מבלי להתעקש על תמונה ציורית, טנזור מוגדר כישות אובייקטיבית עם מרכיבים המשתנים על פי חוק טרנספורמציה שהוא הכללה של חוק הטרנספורמציה הווקטוריאלית אך שומר על שני התכונות העיקריות של אותו חוק. מטעמי נוחות, הקואורדינטות ממוספרות בדרך כלל מ- 1 ל- n, וכל רכיב של טנסור מסומן על ידי אות הכוללת תסריטים עליונים ותסריטים, שכל אחד מהם לוקח באופן עצמאי את הערכים 1 עד n. לפיכך, לטנסור המיוצג על ידי הרכיבים T ab c יהיו n 3 רכיבים כערכים של a, b ו- c יעבדו מ -1 ל- n. סקלרים וקטורים מהווים מקרים מיוחדים של טנסורים, כאשר הראשון בעל רכיב אחד בלבד לכל מערכת קואורדינטות והאחרון בעל n. כל קשר ליניארי בין רכיבי טנסור, כמו 7R a bcd + 2S a bcd - 3T a bcd = 0, אם הוא תקף במערכת קואורדינטות אחת, תקף בסך הכל וכך מייצג מערכת יחסים שהיא אובייקטיבית ובלתי תלויה במערכות קואורדינטות למרות היעדר ייצוג ציורי.
שני טנסורים, המכונים הטנסור המטרי והטנזור העקמומי, מעניינים במיוחד. הטנסור המטרי משמש, למשל, בהמרת רכיבים וקטוריים לעוצמות של וקטורים. לשם הפשטות, יש לקחת בחשבון את המקרה הדו-ממדי עם קואורדינטות פשוטות בניצב. בואו לווקטור V יש את הרכיבים V 1, V 2. ואז על ידי משפט פיתגורס שהוחל על המשולש הימני OAP, הריבוע בגודל V ניתן על ידי OP 2 = (V 1) 2 + (V 2) 2.

חבוי במשוואה זו נמצא הטנזור המטרי. הוא מוסתר מכיוון שהוא כאן מורכב מ- 0 ו- 1 שאינם כתובים עליהם. אם המשוואה נכתבת מחדש בצורה 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, מערך הרכיבים המלא (1, 0, 0, 1) של הטנסור המטרי ניכר. אם משתמשים בקואורדינטות אלכסוניות, הנוסחה עבור OP 2 לוקחת את הצורה הכללית יותרOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, הכמויות g 11, g 12, g 21, g 22 הם המרכיבים החדשים של הטנסור המטרי.
מתוך הטנסור המטרי ניתן לבנות טנזור מורכב, הנקרא טנסור העקמומיות, המייצג את ההיבטים השונים של העקמומיות המהותית של המרחב ה- N ממדי אליו הוא שייך.
לטנסורים יישומים רבים בתחום הגיאומטריה והפיזיקה. ביצירת תורת היחסות הכללית שלו, אלברט איינשטיין טען שחוקי הפיזיקה חייבים להיות זהים, לא משנה באיזו מערכת קואורדינטות משתמשים. זה הביא אותו לבטא את אותם חוקים מבחינת משוואות טנזור. כבר היה ידוע מתורת היחסות המיוחדת שלו, שזמן ומרחב קשורים זה בזה באופן הדוק עד שהם מהווים זמן-חלל-ממדי בלתי ניתן לחלוקה. אינשטיין הניח כי יש לייצג את הכבידה אך ורק מבחינת הטנסור המטרי של זמן מרחב ארבעה ממדי. כדי לבטא את חוק הכבידה היחסי, היו לו כאבני בניין את הטנזור המטרי והטנזור העקמומי שנוצר ממנו. לאחר שהחליט להתגבר באבני הבניין הללו, עצם מיעוטם הוביל אותו למשוואת טנזור ייחודית במהותה לחוק הכבידה, שבו הגרביטציה הופיעה לא ככוח אלא כביטוי לעיקול הזמן-חלל.
בעוד שטנסורים נחקרו קודם לכן, ההצלחה של תורת היחסות הכללית של איינשטיין היא שהולידה את ההתעניינות הרווחת הנוכחית של מתמטיקאים ופיזיקאים בטנורים ויישומיהם.